傳媒誤讀數據 —— 認識疫情數據的常見誤區

疫情爆發至今已逾兩年，儘管疫情影響我們日常生活的每一環節，公眾對疫情的認識和掌握仍然十分有限。原因一方面是因為疫情隨變種病毒的出現而不停改變，專家以科學方法所得的答案往往一轉眼便已跟不上最新的發展。而當社會本身缺乏互信，當權者欠缺認受性，則各種有意或無意的假消息散播更會變得一發不可收拾，為控制疫情增添困難。

在一個理想的民主社會當中，我們會期望傳媒可幫助公眾更知情地參與公眾事務，決定自己的未來。而在訊息紛亂之際，從數據出發本應可讓我們較客觀地分析事實。畢竟數據講求定義，只要定義清晰則應可減少誤解。

不過兩年來，很不幸，傳媒理解和呈現數據的能力明顯受到挑戰，有時越講越糊塗。數據雖然越來越多，卻不見得社會中各種對疫情理解的矛盾有所減少。

蘋果要和蘋果比較

我們從一宗疫苗效用的消息開始談起。去年夏天，網上流傳一份英國政府的研究報告，指已打兩針的感染者住院率比未打疫苗的感染者還要高。有網上名嘴拿著這份報告宣稱數據「令專家不開心」，更聲言打疫苗的風險比不打更大，帖文被廣泛傳播。

這份報告是真的，數據也確實是從報告的資料中推算出來。統計顯示有47008名已接種兩劑疫苗者感染Delta病毒，當中有1355人住院；另有151054名未接種疫苗者感染Delta病毒，當中有2960人住院。換言之，已接種兩劑疫苗者的住院比率是2.88%，未接種疫苗者則是1.96%，即是已接種者反而更高。

在這案例中，數據雖然正確，但結論卻是錯誤的。以上數字是整體情況，但報告也提供了不同年齡層的情況。如果分開年齡層計算，50歲以下已接種兩劑疫苗的感染者和未接種疫苗的感染者，其住院比率分別為0.88%和1.55%；50歲或以上的，則分別為5.27%和19.48%；兩者都是未接種疫苗的感染者住院率較高。

為什麼分開計算是未接種疫苗的感染者住院率較高，合起來計算卻是相反呢？這是因為當時英國的政策是讓年紀較大的先接種疫苗，所以已接種疫苗者當中有很多是年紀較大的人。由於他們本來身體狀況比較差，所以入院的比例也較高。因此，合起來算的結果其實沒有顯示疫苗帶來風險，而是顯示了年齡帶來的風險。沒有考慮這點，便是誤讀數據。

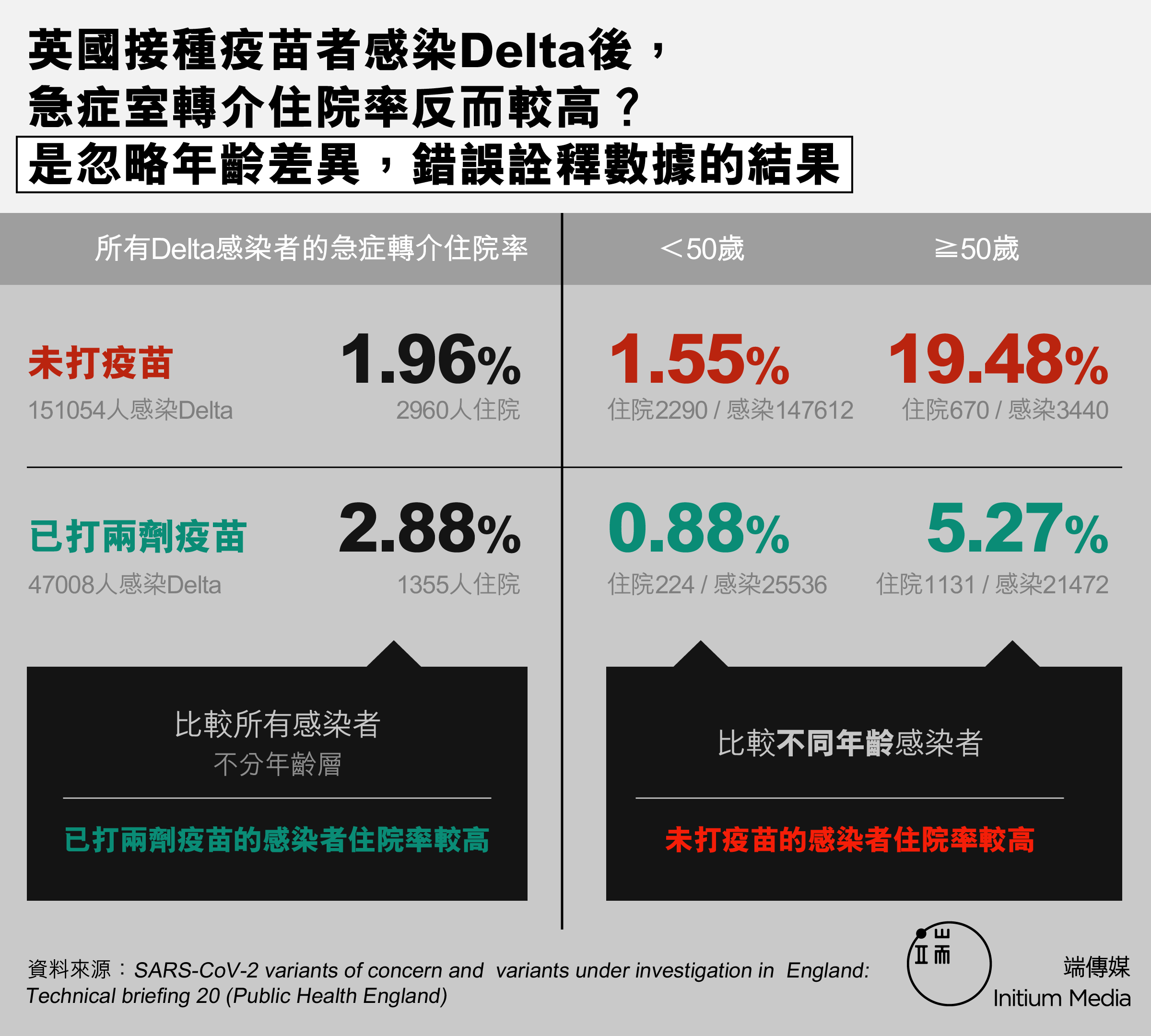
同樣的數據，合起來算和分開算的結果互相矛盾，在數據分析當中相當普遍，學術上稱為「辛普森悖論」（Simpson’s paradox）。它會讓分析結果看起來違反直覺，研究者要小心考慮數據應如何分類和比較才比較貼近事實。換句話說，我們要學懂「蘋果和蘋果比較、橙要和橙比較」。困難的地方，是要先意識到在當前的研究問題下，面前的到底只是一堆生果，還是應分為蘋果和橙。

早前有香港網媒處理葵涌邨的疫情爆發時，亦犯了類似的錯誤。

該網媒統計葵涌邨疫情爆發的數字，發現有55人沒有接種疫苗，曾接種疫苗的則有61人，有接種疫苗者略為多一點（佔整體53%）。即使這些數字本身正確，網媒不加處理就把兩個數字並列出來，仍會產生誤導效果。

事實上，該網媒依此組數字製作的社交媒體圖片迅速被網民轉貼到各網上討論區，被視為「疫苗不能防疫」的所謂「證據」。

回到「蘋果要和蘋果比較」的立足點，上述的理解當然是錯誤的。要知道疫苗能否抗疫，我們需要把整條葵涌邨當中有接種疫苗者和未接種疫苗者分為兩組處理，再看每一組當中染疫者的比例。雖然我們沒有這些數據，但我們可假設葵涌邨的情況和香港的整體相差不太遠，即約有七成居民曾經接種疫苗。如是者，如果疫苗真的不能防疫，我們應預期染疫者當中也該大約有七成曾經接種疫苗。現在染疫者的比例低於七成，在未考慮其他因素影響的前提下，其實恰恰反過來說明疫苗很可能發揮了作用。

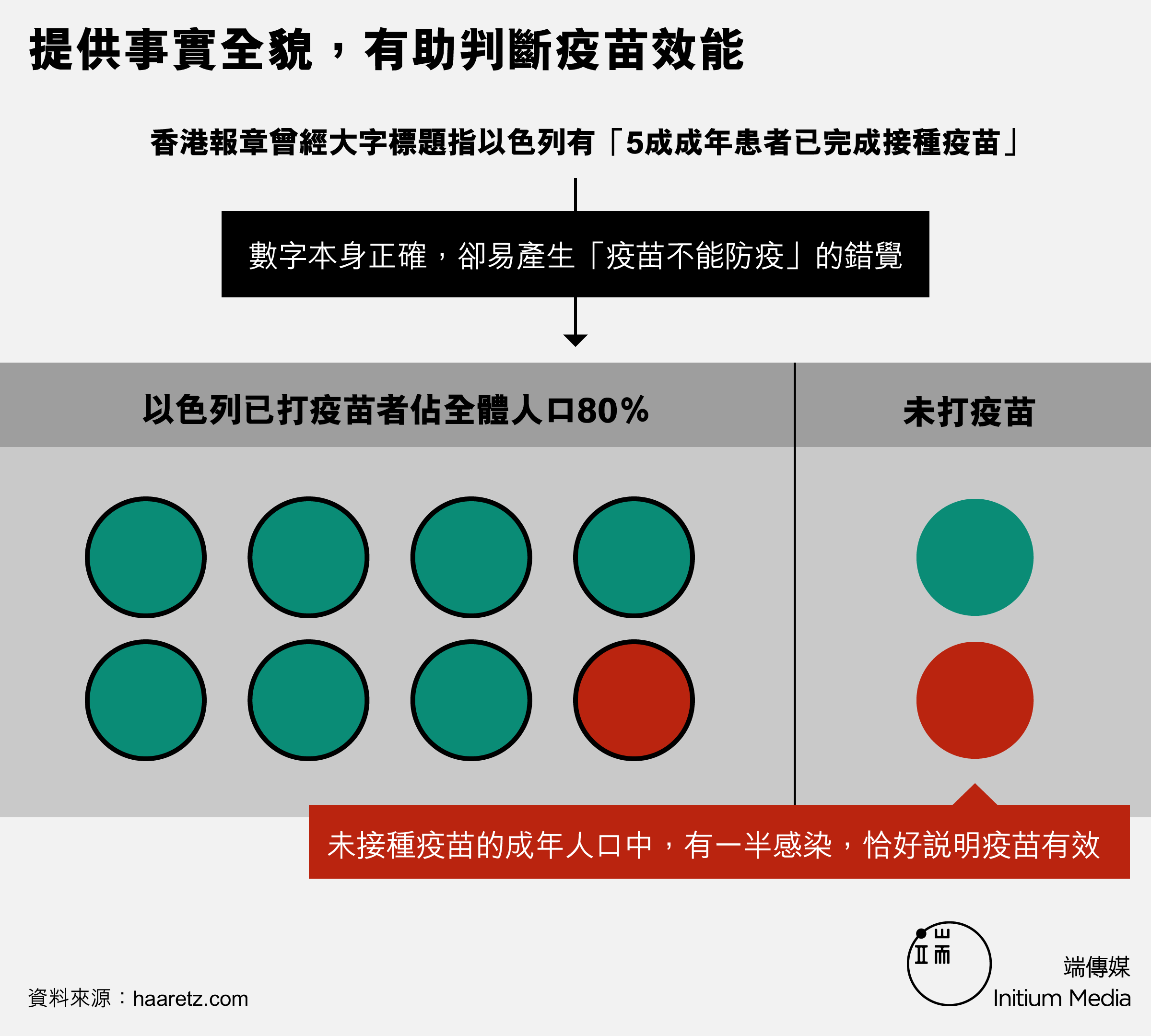
類似的情況，在整場疫情當中不停出現。例如有香港報章曾經大字標題指以色列有「5成成年患者已完成接種疫苗」，雖然這個數字本身正確，但標題卻無助讀者理解當時以色列的疫情，甚至容易產生誤解，讀者一不留神，同樣很容易產生「疫苗不能防疫」的錯覺。

實情是當時未接種疫苗者只佔成年人口的五分之一左右，所以當有一半患者屬未接種疫苗，則同樣恰恰反過來說明疫苗有效。媒體沒有提供這個比較的背景，就好像一宗片面的選擇性報導一樣，只說出事實全貌的一半，還振振有詞說自己沒有半句是假話，其實明明就是新聞專業失當。

數據需要處境

推而廣之，媒體引用任何數據，都應該提供該數據的處境。例如說香港男子組合Error成員郭嘉駿有193厘米高，我們都會得出他身型很高的印象。但我們能有此印象，是因為我們是地球人，知道地球人一般有多高；如果對方是外星人的話，僅僅跟對方說「郭嘉駿有193厘米高」而不同時提供地球人的平均身高，則這句說話本身沒有意義。偏偏在疫情當中，這樣的問題俯拾皆是。

在疫苗接種初期，不少媒體爭相報導民眾接種疫苗後的不良反應，例如有臺灣傳媒就曾以表列方式呈現各縣市的「疫苗開打死亡統計（死因待查）」。這兒最少有兩個問題。第一，既是死因待查，那麼媒體列舉案列時是否最少應該把標準說清（例如說14天內不論任何情況死亡）？畢竟說白了傳媒在此是在發明一套非官方的點算方法，很有必要交代清楚定義。

第二，就算假設定義合理，純粹點算各縣市的數目本身的意義也很有限，因為沒有同時告訴讀者同期各縣市已經施打的疫苗數目。疫苗安全性是一個概率問題，只有分子沒有分母又如何推算概率呢？

即使有了概率，也要提供處境來協助讀者理解。例如有研究說接種阿斯利康疫苗有百萬分之5的機會產生血栓反應，然而一般讀者恐怕很難想像百萬分之5是什麼意思。這時候，我們要把數字化為一些較易理解的概念，例如說如果整個臺北市每人打1次，概率上就會有13人有反應。我們也可以拿其他概率事件作比較，例如臺灣每年交通事故的死亡數字是臺灣人口的百萬分之126，這樣相對起來阿斯利康的百萬分之5算是多還是少，就有個比較的基礎。

提到比例，有些時候我們又不能只看百分比，同時也要與確實數字一起分析。例如在英國一月初Omicron的高峰期時，每日入院人數只是染疫人數的約1%，看起來染疫也不是那麼可怕。但因為Omicron本身的傳染性極高，就算入院的比例很低但因為染疫的人數極多，仍會為醫療系統帶來沉重壓力。一個數字到底是大還是細，總是在一個處境當中回答的。

說起Omicron，坊間有不少輿論認為病毒已經弱化，疫情已和流感無異，這點同樣可以通過提供處境驗證。《紐約時報》統計美國於2022年1月約有6萬人因染疫死亡，而當時Omicron已佔感染個案的99%，說明感染Omicron還是有死亡風險的。那麼6萬人算多還算少？在疫情發生前，美國通常在每年的1月份有大約有26萬人死亡。有這個比較基礎，則說明2022年1月的6萬人其實是個相當龐大的數目了。

善用處境去解說數據還有一個好處：可以為數據要解釋的現象提供額外的評估。例如疫情的死亡率一直備受爭議。有說很多染疫個案沒有被發現或被呈報，所以分母被低估了；又有說很多死亡個案不一定是因為染疫而死，而是同時有其他疾病，所以分子被高估了。有些陰謀論者更認為全世界的政府都在合謀用虛假疫情恐嚇公眾，後面實有其他目的。

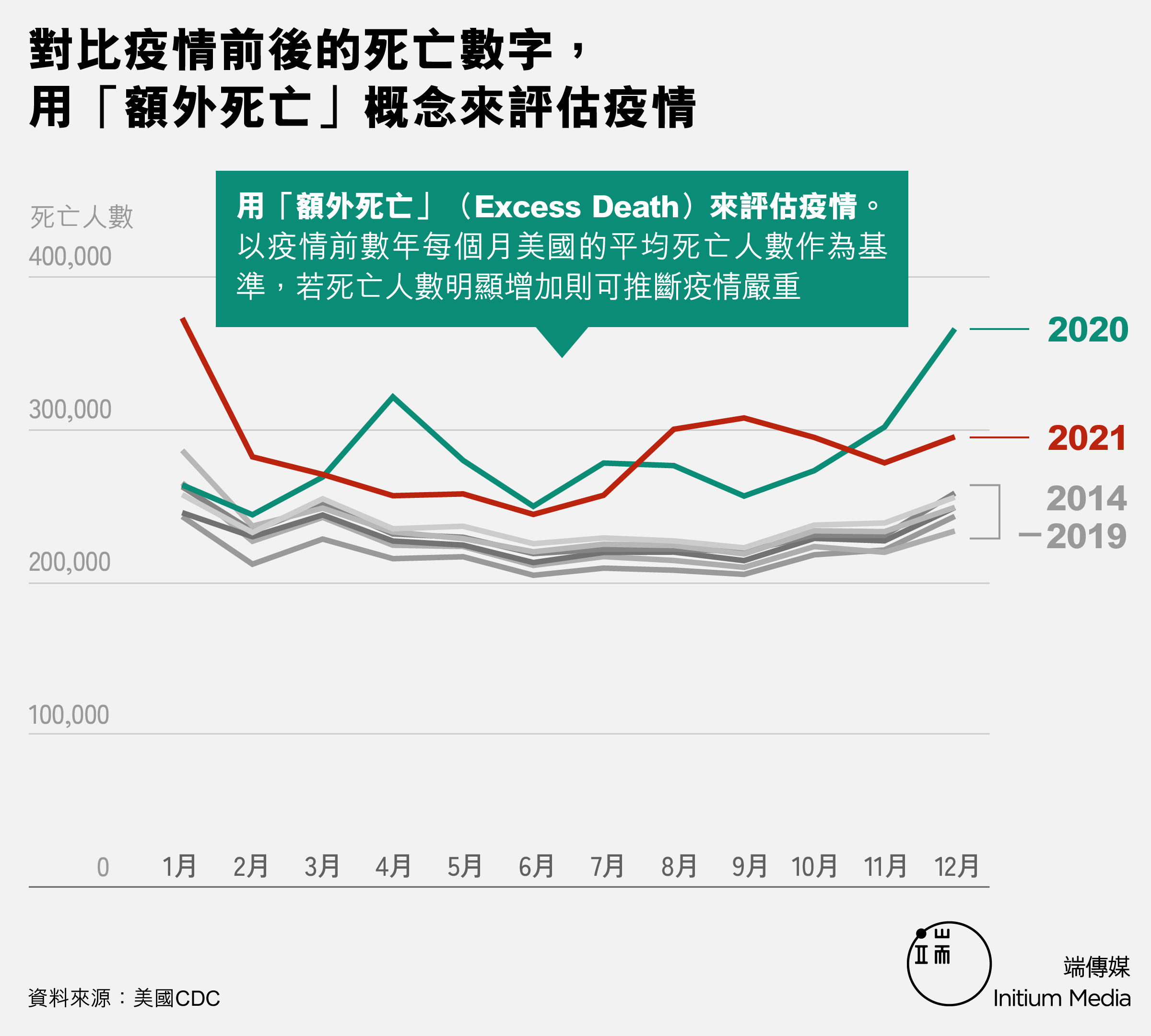
要繞過這些困難，有些外國媒體會用「額外死亡」（Excess Death）來評估疫情。舉個例，我們可以拿在疫情前數年每個月美國的平均死亡人數作為基準，比較疫情開始後每個月的死亡數字。畢竟過去兩年疫情是最明顯的額外死亡因素，如果死亡人數明顯增加則可推斷疫情嚴重，不用擔心會受醫院呈報方法所影響。

教育自己 教育公眾

提到死亡數字，現時不少國家對疫情的理解已開始轉向：不再著重確診數字，而更重視重症和死亡數字。這是因為疫苗普及後確診和重症數字開始脫軌，加上Omicron的重症比例相對較低。例如英國在2022年1月最高的平均每日確診數字約是21萬宗，遠遠比2021年1月的6萬宗要高；但是，2022年1月中的高峰的平均每日死亡數字一直少於300宗，而2021年1月的高峰卻是超過1200宗。一來一回，如果我們只和讀者講英國的確診數字不斷創新高，卻不同時講死亡數字的升幅遠遠較低，則同樣有誤導讀者之嫌。

當然，哪一個時候用哪一個標準去衡量疫情，並無劃一定律。任何的數據最終都是一個被簡化的真實，必然有所偏差，問題是這個偏差是否涉及提問重點，以及有否向讀者清楚交代。很多時候，新聞中的數據呈現出了問題，往往基於媒體本身對數據背後的各種屬性掌握得不夠充分，自己也未搞清那些數字的背後所指，甚至弄出各種笑話。

在疫苗接種的早期，曾有香港網上名嘴質疑政府的疫苗數據作假。他發現政府公佈的疫苗接種數字已有240萬，同時說香港已接種疫苗的比例不足兩成。他按香港700多萬人口計算，認為兩項數字當中必定是有一項是錯誤的。事實是政府公佈的數字是240萬劑而不是240萬人，由於有些人已打了兩針，所以當時的接種人數其實是142萬才對。此外，政府計算接種比例的是以合資格人口算而不是全港人口算，所以分母也不是700多萬。該網上名嘴犯上如此基本的錯誤，未免過於粗心大意。然而類似的簡單理解錯誤，在疫情中數之不盡。

因此，我認為傳媒在疫情面前很有迫切提升自身和社會大眾的數據素養，既要教育自己，也要教育公眾。常說「數據會說話」（The data speaks for itself），專業的數據新聞工作者卻恐怕大多不會同意。數據從選取、分析到呈現，每一步都涉及各種選擇，依靠各種專業判斷；只要略為不留神，就會產生誤導而不自知。

我提議三個傳媒呈現疫情數據時可以立即改善的方向。

第一，處理數據時行文用字應務必力求準確。例如曾有政府官員說疫苗「不一定能防感染」時被傳媒略寫為「不能防感染」，就可以帶來極大的誤解；後者很容易被誤讀為完全不能。事實上，英國的數據顯示接種3針復必泰對Omicron有症狀感染，有約七成保護力；雖然不是百分之百，卻亦絕非毫無作用。

傳媒應教育自己和教育公眾以概率來理解疫情，避免簡單的二分法。正如乘客配帶安全帶也「不一定能」防止乘客於遇上交通意外時受傷，但無阻政府規定乘客配帶，而大多數乘客都會樂於遵守。

第二，提醒公眾注意數據有時會受其他和疫情不相關的因素影響。例如1月初美國單日確診數字曾突破100萬宗，但其實是因為之前數天剛好放假，地方數據上報中央出現滯後，幾天的數據被疊在一起，當時的平均每日確診數字不足50萬宗。美國的大型媒體報導疫情時，會清楚把這些不正常的數值標記出來並作解釋，以免讀者誤解。

類似的情況也可在疫苗接種數字中看到：香港的疫苗接種數量往往是逢星期六特別高，因為很多人覺得星期六接種後可以利用星期日休息。因此，報導相關數字時的常見做法是加入7天平均數，避免一星期內不同天數之間的差異所產生的影響。

第三，提醒公眾注意數據有時未能立即反映後來的影響。例如英國的確診數目在2022年1月1日到達最高峰，但同期死亡數目的最高峰則要到了1月16日才出現，畢竟病人從確診到死亡之間是有時差的。傳媒的責任，就是當確診數目已經上升，死亡數目卻仍然維持低水平之際，提醒讀者不要因為那一刻兩組數字差距巨大而誤以為死亡率低。

類似的情況也可應用在一些知名人士染疫的消息當中。當一些名人公佈自己染疫而又病情輕微，便很容易讓很多人誤以為是必然現象。現實是名人之所以為名人，是因為他們數目有限，但這也暗示他們的代表性亦有限。正如一顆骰子搖6次，結果1至6各出現一次的機會不大；然而如果你搖600萬次，結果1至6的出現次數相若的可能性就很大。有時得承認眼前有限的觀察並不足以讓我們立即跳到結論。

最後，我必須要強調一點：有些事情是數據解決不了的。數據可以告訴你有什麼事情已發生，或可能發生，但不能告訴你什麼事情應該或不應該發生。特別是一些涉及價值觀的問題，數據分析不能完全取代主觀判斷。例如數據可以告訴你採取不同防疫手段對疫情的影響，但不能代替社會回答是否願意接受這些手段。

疫情是科學，但公共政策卻不能離開政治，而政治講求公信。